历年考题分布

本章内容框架

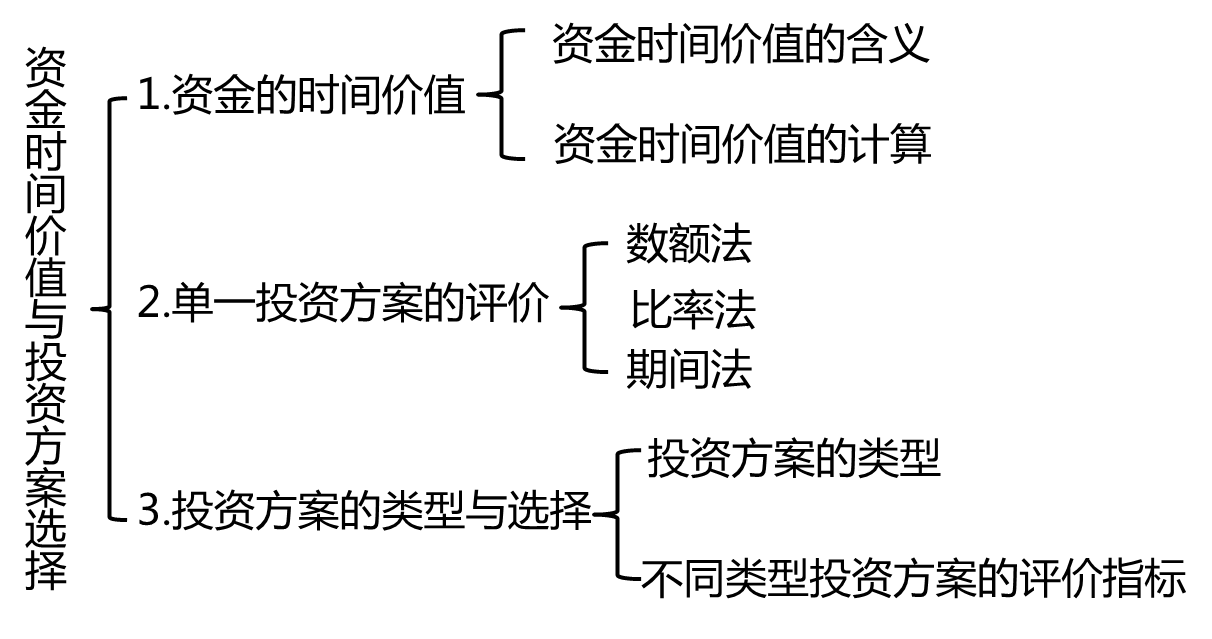
本章特点
考题所占分值大；
理论性强，技术含量高，难度大；
计算题多。

第一节 资金的时间价值

一、资金时间价值的概念
1.资金时间价值的含义
同一资金在周转使用过程中在不同时点上产生的价值差额。

2.资金时间价值变化的原因
（1）通货膨胀、货币贬值
（2）风险因素
（3）周转使用，货币增值

3.基本概念介绍
（1）利率（i） ：相对数指标
（2）利息（I） ：绝对数指标
（3）现值（P）：货币的初始价值，即本金（期初金额）
（4）将来值（F）：货币的未来价值，即本利和（未来值）
（5）年值（A）：是指在一定的时期内，以相同的时间间隔连续发生的等额收付款项

二、资金时间价值的计算
1.单利制
利息和时间呈线性关系，利息不计入本金，计息基础不变，利息固定。（不能反映资金运动的规律性）
F本利和= P×（1+i×n）

2.复利制
是指不仅本金要计算利息,利息也要计算利息,即通常所说的? “利滚利”。 （符合资金时间价值的本质）
F本利和= P（1+i）n

应用分析
将3000元存入银行，年利率为5%，分别按单利、复利计算三年后的本利和为多少？
解：单利 F = P （1＋i×n） =3000×（1＋5%×3）=3000× 1.15=3450（元）
复利 F= P × （1＋i）n = 3000 × （1＋5%）3 =3000 × 1.158=3474（元）


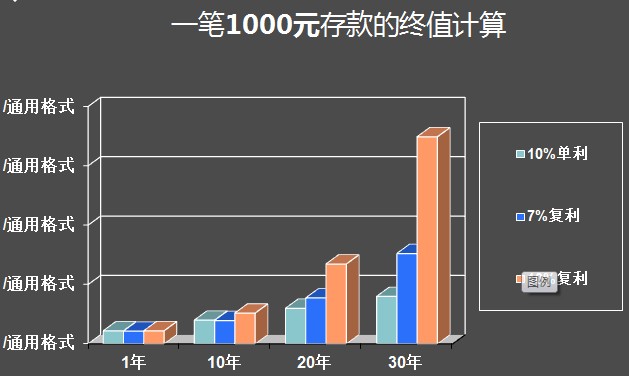
3.现金流量图（辅助计算工具）

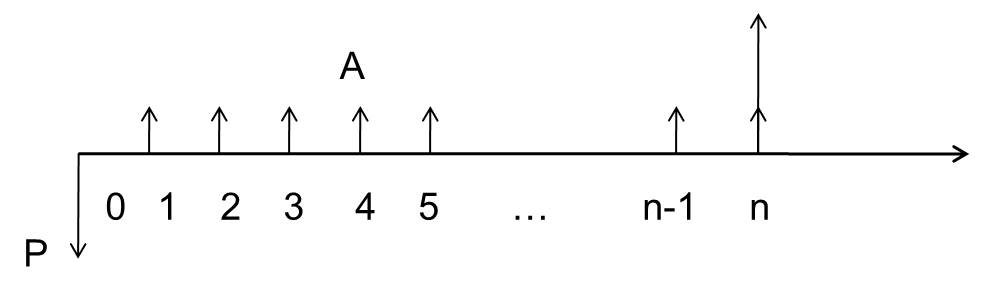
1.一条向右的带箭头的线代表时间轴
2.上面的点代表时间点，起点为0，依次为123…n
3.向上的箭头表示现金流入，向下的箭头代表现金流出
4.箭头的长短与资金量值成正比

4.现金流量计算的基本原则

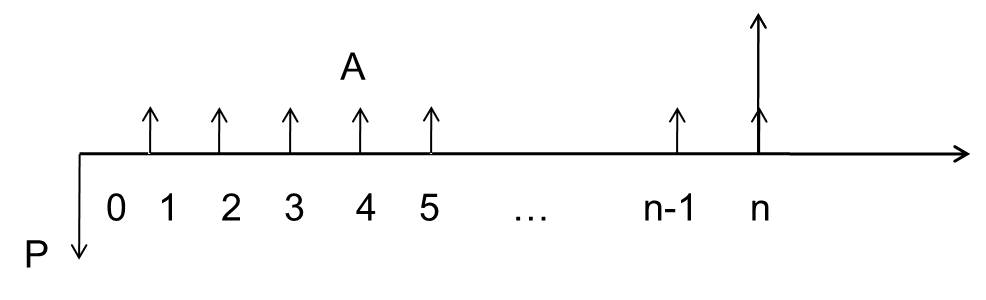
（1）不在同一时点的资金不能比较大小
（2）不在同一时点的资金不能直接相加减
（3）只有将发生在各个点的资金量换算到同一时点，才能比较大小和相加减

5.基本系数
一次支付本利和因数（Ｆ/P，i，n）
一次支付现值因数（Ｐ/Ｆ，i，n）
等额支付将来值因数（Ｆ/A，i，n）
等额支付偿债基金因数（A/Ｆ，i，n）
等额支付现值因数（P/A，i，n）
等额支付资金回收因数（A/P，i，n）

1.一次性支付本利和公式
问题：已知现期的一个支付，在一定利率条件下，求未来某时点的将来值。即已知P、i、n，求F。图示如下：

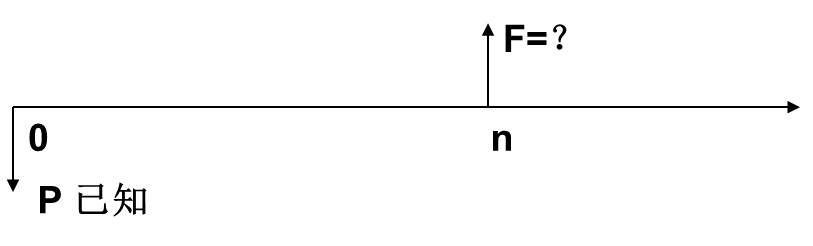
这就是一般复利公式


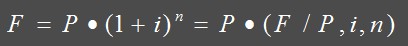
应用分析
某夫妇喜得贵子之时，即投入一笔大学教育基金10000元，以年均5%的收益率投资，当孩子18岁上大学时，这笔基金会有多少呢？
解析:
F = 10000（F/P,5%,18）
= 10000×2.407
=24070（元）

2.一次性支付现值公式
问题：已知将来某个时点的一个支付，在一定利率条件下，求其现在值。即已知F、i、n，求P。图示如下：

它是一般复利公式的逆公式


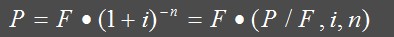
应用分析
某夫妇喜得贵子之时，考虑投入一笔基金用于大学教育，预计孩子18岁上大学时所需各种费用为50000元，设年均收益率为8%,问现在应投入多少？
解析：?
P = 50000（P/F,8%,18）
= 50000×0.2502
= 12510（元）

3.等额支付将来值公式
问题：已知到将来某个时点的各期均有一个等额支付，在一定利率条件下，求其将来值。
即已知A、i、n，求F。图示如下：



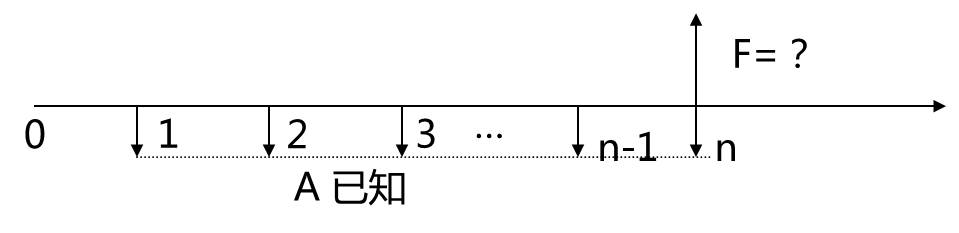
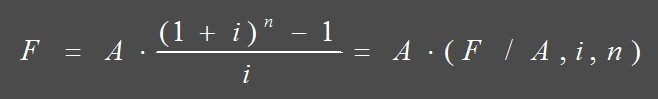
计算公式可由一般复利公式 F = P(1+ i) n推导出来

应用分析
某夫妇喜得贵子之时，考虑建立一项基金用于大学教育，计划每年注入2000元，至孩子18岁上大学时会有多少？设年均收益率为8%。
解析：
F = 2000（F/A,8%,18）
= 2000×37.45
= 74900（元）

4.偿债基金公式
问题：已知到将来某个时点的一个支付，在一定利率条件下，求从现在起到该时点各期的等额支付。即已知F、i、n，求A。图示如下：



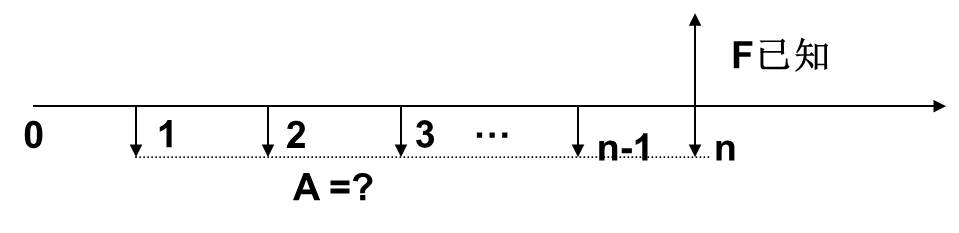
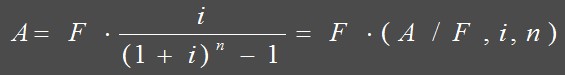
计算公式可由年金本利和公式推导而来

应用分析
某夫妇喜得贵子之时，考虑建立一项基金用于大学教育，预计孩子18岁上大学时所需各种费用为50000元，设年均收益率为8%，问从现在起每年应投入多少？
解析：
A = 50000（A/F,8%,18）
= 50000×0.0267
=1335（元）