4.偿债基金公式

问题：已知到将来某个时点的一个支付，在一定利率条件下，求从现在起到该时点各期的等额支付。即已知F、i、n，求A。图示如下：

计算公式可由年金本利和公式推导而来

应用分析
某夫妇喜得贵子之时，考虑建立一项基金用于大学教育，预计孩子18岁上大学时所需各种费用为50000元，设年均收益率为8%，问从现在起每年应投入多少？
解析： A = 50000（A/F,8%,18）
= 50000×0.0267
=1335（元）

5.等额支付现值公式
问题：已知到将来某个时点的各期均有一个等额支付，在一定利率条件下，求其现值。即已知A、i、n，求P。图示如下：



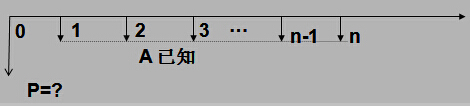
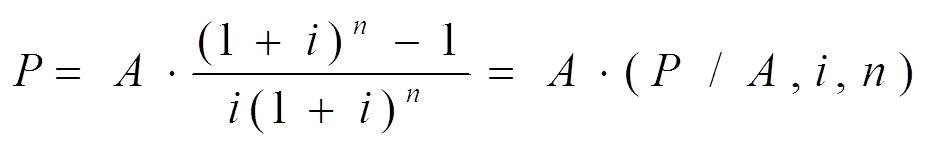
计算公式可由整付现值公式 P = F（1+ i）－n推导而来

应用分析
某人向建行申请10年期购房按揭贷款，他每年的还款能力为8000元，年利率为5%，问他可以向银行贷多少？
解析： P = 8000（P/A,5%,10）
= 8000×7.722
=61776（元）

6.资金还原公式
问题：已知现在有一个支付，在一定利率条件下，求到将来某个时点各期的等额支付。即已知P、i、n，求A。图示如下：

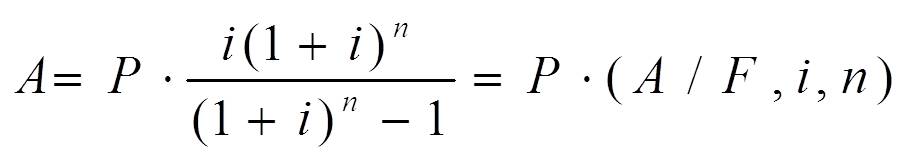
计算公式可由年金现值公式推导出来

特殊情况当n ∞时 A=P·i

应用分析
某人向建行申请15年期购房按揭贷款12万元，年利率为5%，求他每年的还款额？
解析： A = 120000（A/P,5%,15）
= 120000×0.09634
= 11560.8（元）

7.假定条件
（1）初期投资发生在方案的寿命期初；
（2）方案实施的经常性收益和费用假定发生在计息期的末期；
（3）本期的期末是下期的期初；
（4）现值P是当前期间开始时发生的；
（5）年值A是在考察期间间隔发生的；当问题包括P和A时，系列的第一个A是在P发生一个期间后的期末发生的；当问题包括F和A时，系列的最后一个A与F同时发生的。

8.解题步骤
第一步，审题。复杂题必须画出现金流量图帮助理解。（注意：现金流量图的三要素：大小 (现金数额)、方向(现金流入或流出)和作用点(现金发生的时间点)。一定要绘制正确）。

第二步，确定换算关系。审题后确定其经济活动的内涵是哪两个值之间的换算，写出关系式，如A=P(A/P，i，n)，这需要熟练掌握六种换算

第三步，审查条件。题中的条件与公式换算的假定条件是否一致，如不一致，则需调整换算关系式

第四步，检查一致性。注意i与n的内涵是否一致：如果i是年(季、月)利率，则n就是以年(季、月)为标准的计息期；如果没有明确告知，则季利率等于年利率除以4，月利率等于年利率除以12。

第五步，计算。将已知数据代入关系式中计算

应用分析
例1.有一对父母为两个孩子的大学教育攒钱。他们相差两岁，大的将在15年后上大学，小的则在17年后。估计届时每个孩子每年学费将达到21000元。年利率为15%，那么这对父母每年应存多少钱才够两个孩子的学费？现在起一年后开始存款，直到大孩子上大学为止。
A(F/A,15%,15)=21000×(P/A,15%,4)(1+15%)+21000×
(P/A,15%,4)(P/F,15%,1) 
故A=2544.87元 

例2. 某人从银行借款10万元，借款期为5年，若年利率为6%，则5年后按复利和单利计息时利息总额的差值是（）万元。已知：( F/P，6%，5)=1.338。
A.0.25 B.0.28 C.0.35 D.0.38
差额=P ( F/P，6%，5)- P(1+5*6%)=10*0.038=0.38
故差额= 0.38万元