1Z101000 工程经济

1Z101010 资金的时间价值的计算及应用

二 、终值和现值的计算
（一）一次支付的终值和现值计算
1.一次支付现金流量

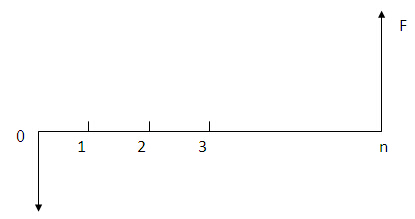
2.终值计算 (已知 P 求 F)
F＝P（1＋i)n
1＋i)n 称为一次支付终值系数 , 用（F/P, i, n）表示
F＝P（F/P, i, n）

例：某人借款 10000 元 , 年复利率 i=10% , 试问 5 年末连本带利一次需偿还若干 ?
解 : F＝P（1＋i）n =10000×（1＋10%）5 =16105.1 元

3.现值计算(已知 F 求 P)
P＝F（1＋i)-n
（1＋i)-n 称为一次支付现值系数 ,也可叫折现系数或贴现系数,用 (P/F, i, n)表示。
F＝P（F/P, i, n）
例：某人希望5年末有 10000 元资金，年复利率 i=10%，试问现在需一次存款多少 ?
解 : P＝F（1＋i)-n = 10000×（1＋10%)-5=6209 元
 从上可以看出：现值系数与终值系数是互为倒数。

（二）等额支付系列的终值、现值计算

1. 终值计算（已知 A，求 F）
等额支付系列现金流量的终值为 :

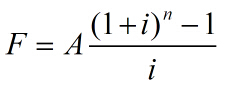
[（1＋i）n－1]/i 称为等额支付系列终值系数或年金终值系数 , 用 (F/A，i，n)表示。

F=A(F/A，i，n)。

例：若 10 年内，每年末存 1000 元，年利率 8%, 问10 年末本利和为多少 ?

解 :


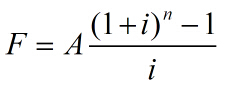
＝1000×[（1＋8%）10－1]/8%
＝14487

2. 现值计算（已知 A 求 P）

 

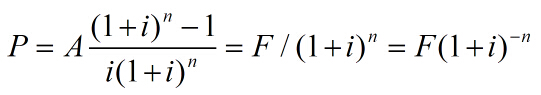
[（1＋i）n－1]/i（1＋i）n 称为等额支付系列现值系数或年金现值系数 , 用 (P/A，i，n)表示。
P＝A(P/A，i，n)

例：如期望 5 年内每年未收回 1000 元，问在利率为 10% 时，开始需一次投资多少 ?
解 :

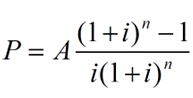
＝1000×[（1＋10%）5－1]/10%（1＋10%）5
＝3790. 8 元

影响资金等值的因素有三个：金额的多少、资金发生的时间长短、利率(或折现率) 的大小。

如果两个现金流等值，则在任何时刻价值必相等

双方出资一般情况下应坚持按比例同时出资，否则应进行等值换算。

应用分析

1．下列是年金现值系数表示符号的是（ ）。
A．（A／F，i，n） 
B．（A／P，i，n） 
C．（F／A，i，n） 
D．（P/A，i，n）
答案：D

2．某施工企业拟对外投资，但希望从现在开始的5年内每年年末等额回收本金和利息200万元，若按年复利计算，年利率8%，则企业现在应投资（ ）万元。
已知：（P/F，8%，5）=0.6808
（P/A，8%，5）=3.9927
（F/A，8%，5）=5.8666
A．680.60 B．798.54
C．1080.00 D．1173.32
答案：B

3．某企业现在对外投资200万元，5年后一次性收回本金和利息，若年基准收益率为i，已知：(P /F，i，5)=0.6806，(A / P，i，5)=5.8666，（F / A，i%，5）=0.2505，则总计可以回收( )万元。
A．234.66 B．250.50
C．280.00 D．293.86
答案：D

4．某人连续5年每年年末存入银行20万元，银行年利率6％，按年复利计息，第5年末一次性收回本金和利息，则到期可以收回的金额为( )万元。
A．104．80 B．106．00
C．107．49 D．112．74
答案：D
解析：20（F/A，6%，5）=112.74
（2014年出了同样的题）

5. （2013）某施工企业投资200万元购入一台施工机械，计划从购买日起的未来6年等额收回投资并获取效益。若基准收益率为10%，复利计息，则每年末应获得的净现金流入为（ ）万元。
A.200×（A/P，10%，6）
B.200×（F/P，10%，6）
C.200×（A/P，10%，7）
D.200×（A/F，10%，7）
答案：A

6．现在的100元和5年后的248元两笔资金在第2年末价值相等，若利率不变，则这两笔资金在第3年末的价值（ ）。
A．前者高于后者
B．前者低于后者
C．两者相等
D．两者不能进行比较
答案：C

1Z101013名义利率与有效利率的计算

利率周期通常以年为单位，当计息周期小于利率周期时，就出现了名义利率和有效利率。
一、名义利率的计算
名义利率 r 是指计息周期利率 i 乘以利率周期内的计息周期数 m 所得的利率。
即：r＝i×m
二、有效利率的计算
有效利率也称实际利率，包括：
1. 计息周期有效利率,即计息周期利率i：
i＝r / m

2. 年有效利率,即年实际利率。

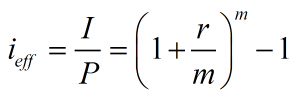
例：
1.按月计息，月利率为1%，则年名义利率和有效利率分别是多少
年名义利率r＝i×m=1%×12=12%
年有效利率ieff=(1+1%)12-1=12.68%

2.按季度计息，年利率为12%，则半年名义利率和有效利率分别是多少
季度利率i=12%/4=3%
半年名义利率r＝i×m = 3%×2 = 6%
半年有效利率ieff = (1+3%)2-1 = 6.09%

由此可见，有效利率和名义利率的关系实质上与复利和单利的关系一样。

应用分析
例题
1．已知年名义利率是8%,按季计息,则计息期有效利率和年有效利率分别为（ ）。
2.00%，8.00%
2.00%，8.24%
2.06%，8.00%
2.06%，8.24%
答案：B （2014年出了同样的题）

2．（2011）某企业从金融机构借款100万元，月利率1%，按月复利计息，每季度付息一次，则该企业一年需向金融机构支付利息（ ）万元。
A.12.00
B.12.12
C.12.55
D.12.68
答案：B
解析：月利率1%，按月复利计息，季度利率为：（1+1%）^3-1=3.03%
每季度付息一次。（单利）一年四季。 100×3.03%×4=12.12

3．（2013）某施工企业向银行借款250万，期限2年，年利率6%，半年复利计息一次，第二年末还本付息，则到期企业需支付给银行利息为（ ）万元。
A.30.00
B.30.45
C.30.90
D.31.38
答案：D

4.（2014）关于年有效利率和名义利率的说法，正确的有 （ ）。
A．当每年计息周期数大于1时，名义利率大于年有效利率
B．年有效利率比名义利率更能准确反映资金的时间价值
C．名义利率一定，计息周期越短，年有效利率与名义利率 差异越小
D．名义利率为r，一年内计息m次，则计息周期利率为 r*m
E．当每年计息周期数等于1时，年有效利率等于名义利率
答案：BE